There is an option of comparing the “live” forecast with forecasts produced using other in-data. Up to five different weather stations can be connected to each forecast. These weather stations, which are numbered from 1 to 5, can either be reserved for weather forecasts from a specific weather supplier or for weather stations with a geographic spread. Each weather forecast gives rise to a load forecast, which can then be co-weighted in accordance with the user’s wishes.

To be able to evaluate a specific weighting, click on  above “Selections” and click again on  at the bottom left of the dialog box displayed. Here, you have the option to determine the weighting manually or to allow the program to find an optimum weighting based on incremental linear regression. In our first example, we will determine the weights ourselves and so we select “Manual”.  

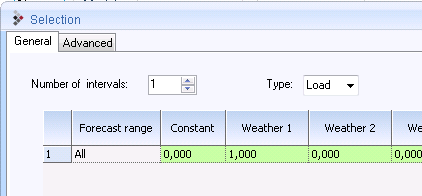
We set “Number of intervals” to 1 and type 0 into the row below; except for ‘Weather 1’, for which we will set a weight of 1.

Choose a name for this weighting, e.g. “Weather 1”, then click on OK.

This weighting that you just created can now be selected. We can now repeat the steps above and create weightings where each and every one of the included weather forecasts has 100% and then select all entries in a “Selection” collection which we can call “All separate”.

If we combine “All separate” with the extract selection “elspot”, five curves are displayed in the diagram (with the exception of the result curve), and if we use the extract selection “elspot+ 2 days back” (see above) instead, we have ten different forecasts to evaluate. If we have exported and unadjusted checked as well, this number increases to 14. For example, we then evaluate both the unadjusted forecast and the exported forecast two days and one day before the evaluated day.

.

Besides evaluating the various weather forecasts individually, we can of course select any choice of weighting, e.g. allow each and every one of the forecasts to contribute 20 %, i.e. 0.2 as a weight. In the next section, we will look at how to allow the program to find an optimal weighting by using step-wise multiple linear regression.