This is a model intended for district heating forecasts where not only the historical production/load is used but also the historical forward temperature. These values are imported and stored in an aio5-file. The forecasting process first starts by modelling the forward temperature based on previous values of the forward temperature, the momentaneous outdoor temperature, and a weekday/holiday hourly pattern modelled by sinus and cosinus functions of the time of the day. An example of an estimated forward heat temperature model is:

The model then calculates the forecasted forward heat temperature and uses the difference between two consecutive values as a new predictor together with the previous heat power values, outdoor temperature and sinus/cosinus functions of the time of day when modelling the heat power. An example of an estimated heat power model is:

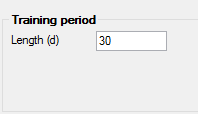
The model uses adaptive least squares when estimating the coefficients with an Attenuation factor or forgetting factor which damps the influence of old values. The length of the training period must be specified.

The longer training period, the more impact will the forgetting factor have on the influence of older values, so that an estimated model with a training period of 40 days will only marginally differ from an estimated model with a training period of 50 days.