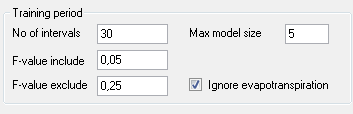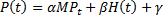
Den statistiska delen av Achelous antar att effekten från ett kraftverk timme t av prognosen kan skrivas som
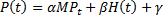
där MPt tas fram som ett medelvärde för timme t av prognosen och αH(t) skattar känsligheten för skillnader i tillrinning.
MPt : Först bestäms en period vilkens längd i dagar man anger i ”Length (d)”. Alla delinterval av längden ”Compare (h)” jämförs med perioden som omedelbart föregår prognosen.
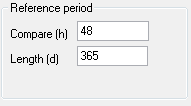
Dessutom jämförs tillrinningen mellan prognosperioden och perioden efter delintervallet. Som en grov uppskattning av vad tillrinning i mm motsvaras i produktion delas medelproduktionen under träningsperioden med medeltillrinningen. Tillrinningens genomslag från 0 till 100% (0 till 1) ställs även in manuellt i modellinställningen nedan under ”Runoff factor”
Delintervallen rangordnas efter hur lika effekt/tillrinningsmönstren är utifrån den totala MAE
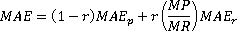
Där r är ”Runoff factor”, MAEp medelabsolutfelet för produktionen, MP/MR medelproduktion delat med medeltillrinning som ”översätter” tillrinningen till produktion och slutligen MAEr som är medelabsolutfelet för tillrinningen. För prognosperioder med monotont icke-växande tillrinning spärras delintervall som efterföljs av perioder där det största absolutbeloppet av skillnaden mellan två värden motsvaras av en ökning av produktionen.
För de intervall som påminner mest om mönstret som föregår prognosperioden beräknas timme för timme medelvärden för de efterföljande timmarna som ska motsvara prognosperioden. Antal intervall som ska inkluderas bestäms av värdet i ”No of Statistisk del intervals” (Se nedan). Resultatet blir dels medelproduktionen timme för timme, dels tillrinningen timme för timme som sedan ska användas i nästa steg.
βH(t): Tillrinningens påverkan på effekten både momentant och eftersläpande beräknas genom att först skapa sekundära prediktorer av tillrinningen som både är förskjutna i tid och utjämnade genom glidande medelvärden. Dessa används som förklarande variabler tillsammans med MPt i en regression vars inställningar visas nedan (Mer om regressionen kan hittas under Aiolos och Cilia-modellerna). För att stänga av regressionen helt kan ”Max model size” sättas till -1.