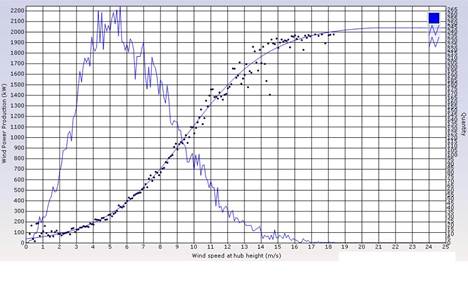
Figur 2: Empirisk effektkurvaAiolos Wind Power använder sig av en så kallad ”gray-box” eller grålåde-modell, dvs en modell som både använder sig av fysikaliska samband såväl som statistiska data. Skattningen av de statistiska parametrarna kan ske regelbundet för att anpassa modellerna till ny data, antingen på användarens initiativ eller schemalagt. Indata till modellen består av prognoser av ett antal meteorologiska variabler som kan anses påverka effekten. Dessa är:
•Vindhastigheten på 80 m höjd
•Vindhastigheten på 10 m höjd
•Vindriktningen på 80 m höjd
•Temperaturen på 2 m höjd
•Temperaturen på 80 m höjd
•Lufttrycket vid markytan
Dessa variabler är uppräknade i ordning efter deras påverkan på effekten. Grundvariablerna är de två vindhastigheterna. Dessa används dels till att skatta en modell för hur vindhastigheten förändras med höjden över marken, en så kallad vindprofil, dels till att interpolera vindhastigheten med hjälp av den skattade vindprofilen till önskad höjd. Varierande vindstyrkor över rotorarean komplicerar beräkningarna i och med att effekten av den passerande vinden bör integreras över hela arean samtidigt som man bör ta hänsyn till hur vindkraftverkets effektivitet förändras med dessa skillnader. I prognossammanhang räcker dock en något förenklad modell, där vi antar att vindhastigheten är konstant över hela rotorarean, och där denna hastighet interpoleras fram nära navhöjden på det aktuella vindkraftverket.
Denna hastighet justeras med hjälp de tre sist uppräknade variablerna för att ta hänsyn till densitetens påverkan på effekten. Denna justerade vindhastighet blir den förklarande variabeln i träningen av modellen. I figur 1 visas resultatet av en träning. x-axeln visar prognostiserad vindhastighet och y-axeln visar uppmätt produktion. De blå punkterna är medelvärden av den uppmätta produktionen för olika vindhastighetsintervall som vardera är 0,1 m/s långa. På all tillgänglig historik anpassas sedan genom icke-linjär regression en empirisk effektkurva fram, som även den är iritad i diagrammet och som synes följer punkterna tätt. Denna kurva är den statistiska motsvarigheten till de teoretiska effektkurvor som tillhandahålls av tillverkare av vindturbiner. Den andra hackigare kurvan visar antalet observationer som faller inom varje prognostiserat vindintervall.
Figur 2: Empirisk effektkurva
Varför skiljer sig de teoretiska och de empiriska effektkurvorna åt? Dels bygger de empiriska effektkurvorna på vindhastighetsprognoser och inte uppmätt vind. Dessa kan ha systematiska avvikelser från den verkliga vinden bland annat beroende på:
•Prognostiserad vindhastighet
•Prognostiserad vindriktning
vilket kan ha förklaringar i tex terrängen i området, omgivande höjdskillnader och inverkan av andra vindkraftverk i närheten, för att nämna några möjliga orsaker. De första felen minimeras med hjälp av empiriska effektkurvor medan AWP försöker minimera felen beroende av vindriktning genom att separera observationerna i olika vindriktningsintervall och räknar fram en separat effektkurva för vart och ett av intervallen. AWP väljer automatiskt det optimala antalet vindriktningsintervall från 1 upp till 12 olika. De teoretiska effektkurvorna gäller vid en viss luftdensitet, så en uppmätt vindhastighet motsvarar inte alltid samma produktion. AWP justerar automatiskt som nämnts tidigare för densitetsskillnader i luften.
I allmänhet syftar träningen till att minimera framtida kostnader för balansansvariga aktörer på elmarknaden. Med tanke på dessa kostnader är ett naturligt kvalitetsmått för prognoserna medelabsolutfelet(eng. mean absolute error, MAE). Denna definieras som
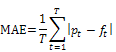
Där T är antalet observationer och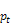 
faktiskt utfall jämfört med prognosen
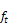samma timme.
En aspekt som är viktig att ta hänsyn till är skeva
produktionsfördelningar. Antag att vi har plottat den historiska produktionen
mot de historiska vindhastighetsprognoserna. Om vi tex inskränker oss till
att betrakta fördelningen av produktionen för prognostiserade vindstyrkor
under 3 m/s kommer fördelningen av utfall att vara skev uppåt, dvs större delen
av observationerna kommer att ligga nära noll med en ”svans” uppåt, då prognosen
uppenbarligen har underskattat vindstyrkan. Att för detta vindstyrkeintervall
välja en optimal produktionsprognos är beroende på vilken så kallad
kostnadsfunktion man vill minimera. En klassisk kostnadsfunktion vid tex linjär
regression är felens kvadratsumma eller roten ur felens kvadratsumma (eng.
Root of mean squared errors, RMSE). Givet T observationer av uppmätt
produktion 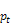med tillhörande prognosvärden 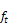definieras RMSE som
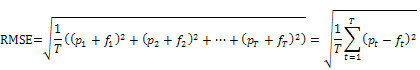
Av definition minimeras RMSE ifall vi väljer det aritmetiska medelvärdet av alla produktionsutfall som produktionsprognos där vindprognosen visar under 3 m/sl. Ett alternativ till medelvärdet är medianen som definieras som det mittersta värdet i en serie värden ordnade i storleksordning.. Medianen minimerar per definition MAE, och i exemplet ovan kommer medelvärdet dras upp av fördelningens svans, vilket ökar MAE. En modell som vill minimera RMSE, kommer att därför under långa perioder med lugnt väder överskatta produktionen som kompensation för de förhållandevis få tillfällen då den rejält underskattar produktionen. För att komma ifrån denna oönskade effekt använder sig Aiolos av en trimmad regression, där i varje vindintervall en viss procentsats av de högsta och de lägsta värdena tas bort. Resultatet blir en anpassad regressionskurva som drar sig från medelvärdet mot medianen i varje vindintervall. Dessutom bidrar trimningen till att göra modellerna mindre känsliga för felaktiga värden och ej kända driftsavbrott.
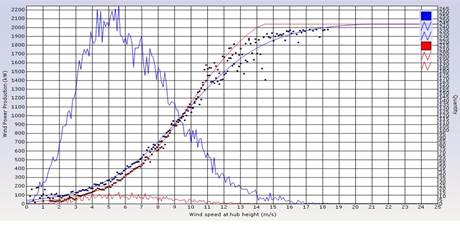
Figur 2: Medianer röda punkter, medelvärden i blått.
I figur 3 visas en sammanfattning av modellprocessen. I rutan längst upp till vänster står förkortningen NWP (eng. Numerical Weather Prediction), som syftar på de väderprognoser som ligger till grund för produktionsprognoserna. I steg för steg nedåt interpoleras variablerna till rätt position och höjd, justering för luftdensitet görs, och slutligen genom ett antal empiriska effektkurvor uppnås en modell för produktionen.
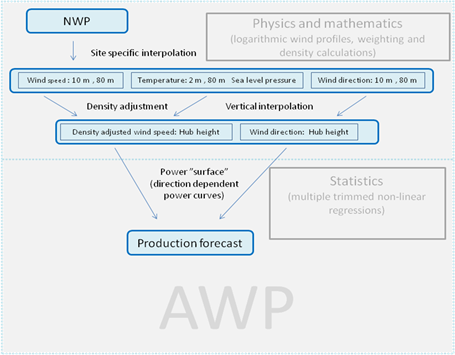
Figur 3: Sammanfattning av modellskapande i AWP